Introduction to Tree Data Structures

A tree is a hierarchical data structure that consists of nodes connected by edges. It is similar to a real-life tree, where the root is the base of the tree, and the branches connect to other nodes, which represent the leaves. A tree data structure is a collection of nodes, where each node has a value and a set of references to its children nodes.

Trees are efficient data structures for representing hierarchical data, such as file systems, organization charts, and family trees. They provide fast access to the data and enable quick insertion, deletion, and search operations. In this article, we will discuss the terminology, types, applications, and operations of tree data structures.

Tree Data Structure

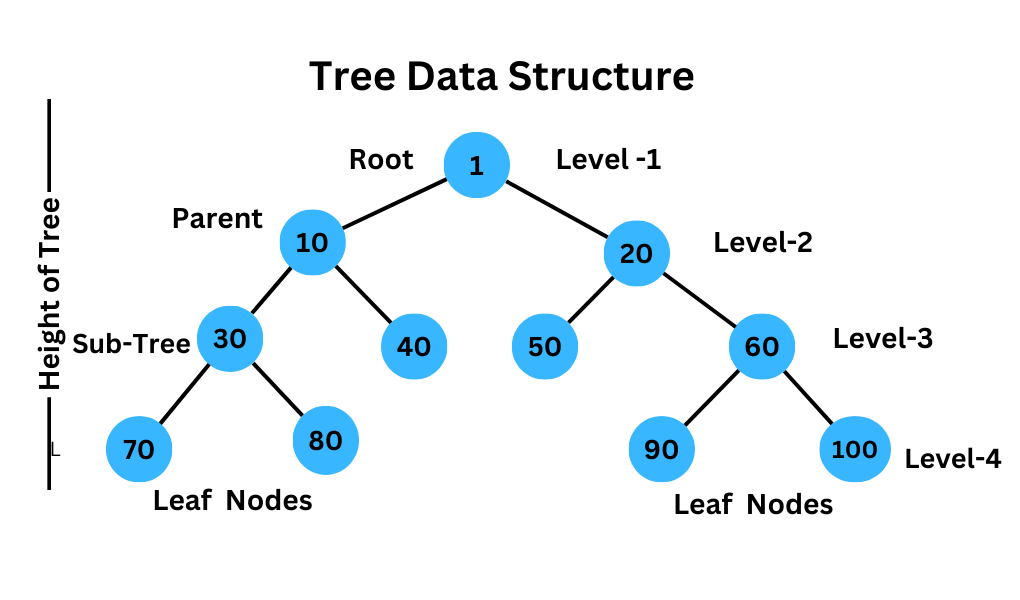
Terminology of Trees

Before we dive into the types of trees, let’s discuss the basic terminology of trees.

Root

The root is the topmost node of a tree. It has no parent node, and it is the starting point of the tree.

Node

A node is a single element in a tree. It contains a value and a set of references to its children nodes.

Edge

An edge is a connection between two nodes in a tree.

Leaf

A leaf is a node that has no children.

Parent and Child

A node that has a child is called a parent node, and the node it points to is called a child node.

Height and Depth

The height of a tree is the length of the longest path from the root to a leaf node. The depth of a node is the length of the path from the root to that node.

Degree

The degree of a node is the number of children it has.

Subtree

A subtree is a portion of a tree that contains a node and all of its descendants.

Path

A path is a sequence of edges that connect two nodes in a tree.

Types of Trees

There are many types of trees, each with its own advantages and disadvantages. In this section, we will discuss some of the most common types of trees.

Binary Tree

A binary tree is a tree where each node has at most two children. The left child is smaller than the parent, and the right child is greater than the parent.

Binary Tree Data Structure

AVL Tree

An AVL tree is a self-balancing binary search tree. It ensures that the height difference between the left and right subtrees is at most one, which makes it more efficient than a regular binary tree.

Red-Black Tree

A red-black tree is another self-balancing binary search tree that uses color to balance the tree. Each node is colored either red or black, and the tree is balanced to ensure that no two adjacent nodes are red.

Trie

A trie is a tree-like data structure that is used to store strings. Each node in a trie represents a single character in a string, and the root node represents an empty string.

Heap

A heap is a tree-based data structure that is used to maintain a collection of elements. It is typically used to implement priority queues, where the elements with the highest priority are removed first.

Applications of Tree Data Structures

Tree data structures have many applications in various fields, such as:

File Systems

Tree data structures are commonly used to represent file systems. The root node represents the file system’s base directory, and the child nodes represent the directories and files within the system.

Compilers

Compilers use tree data structures to represent the syntax of programming languages. The root node represents the program’s starting point, and the child nodes represent the program’s statements and expressions.

Database Management Systems

Tree data structures are used in database management systems to store indexes for quick data retrieval. The root node represents the starting point of the index, and the child nodes represent the indexed values.

Artificial Intelligence

Tree data structures are used in artificial intelligence to represent decision trees. The root node represents the starting point of the decision-making process, and the child nodes represent the possible outcomes.

Computer Networks

Tree data structures are used in computer networks to represent the hierarchical structure of the network. The root node represents the network’s base station, and the child nodes represent the subnetworks and devices within the network.

Tree Operations

Tree data structures support many operations, including:

Traversal

Tree traversal refers to visiting all the nodes in a tree in a specific order. There are two main types of tree traversal: depth-first traversal and breadth-first traversal.

Insertion

Insertion refers to adding a new node to a tree. The new node is inserted in the appropriate location based on its value.

Deletion

Deletion refers to removing a node from a tree. The node is removed, and the tree is restructured to maintain its properties.

Searching

Searching refers to finding a node with a specific value in a tree.

Sorting

Sorting refers to arranging the nodes in a tree in a specific order.

Advantages of Tree Data Structures

Tree data structures have many advantages, such as:

  • Efficient data retrieval and search operations
  • Quick insertion and deletion of nodes
  • Easy representation of hierarchical data
  • Versatility in terms of types of trees and operations
  • Flexible memory usage

Conclusion

Tree data structures are an essential concept in computer science and programming. They are widely used in various fields, such as database management systems, operating systems, compilers, and more. In this article, we discussed the terminology, types, applications, and operations of tree data structures. We hope that this comprehensive guide has provided you with a better understanding of this critical data structure.

FAQs

  1. What is a tree data structure? A tree is a hierarchical data structure that consists of nodes connected by edges.
  2. What are the advantages of tree data structures? Tree data structures have many advantages, such as efficient data retrieval and search operations, quick insertion and deletion of nodes, and easy representation of hierarchical data.
  3. What are some applications of tree data structures? Tree data structures are used in various fields, such as file systems, compilers, database management systems, artificial intelligence, and computer networks
JOIN OUR NEWSLETTER
And get notified everytime we publish a new blog post.