Introduction to Trie Tree

Trie tree, also known as Prefix tree, is a tree-based data structure used to store and search for strings efficiently. It is particularly useful when you need to perform operations on a large set of strings.

What is Trie Tree ?

Trie tree, also known as Prefix tree, is a tree-based data structure used to store and search for strings efficiently. It is named after the word ‘retrieval’, as it can be used to retrieve stored data by traversing a tree-like structure.

Trie Tree Data Structure By Learn Loner

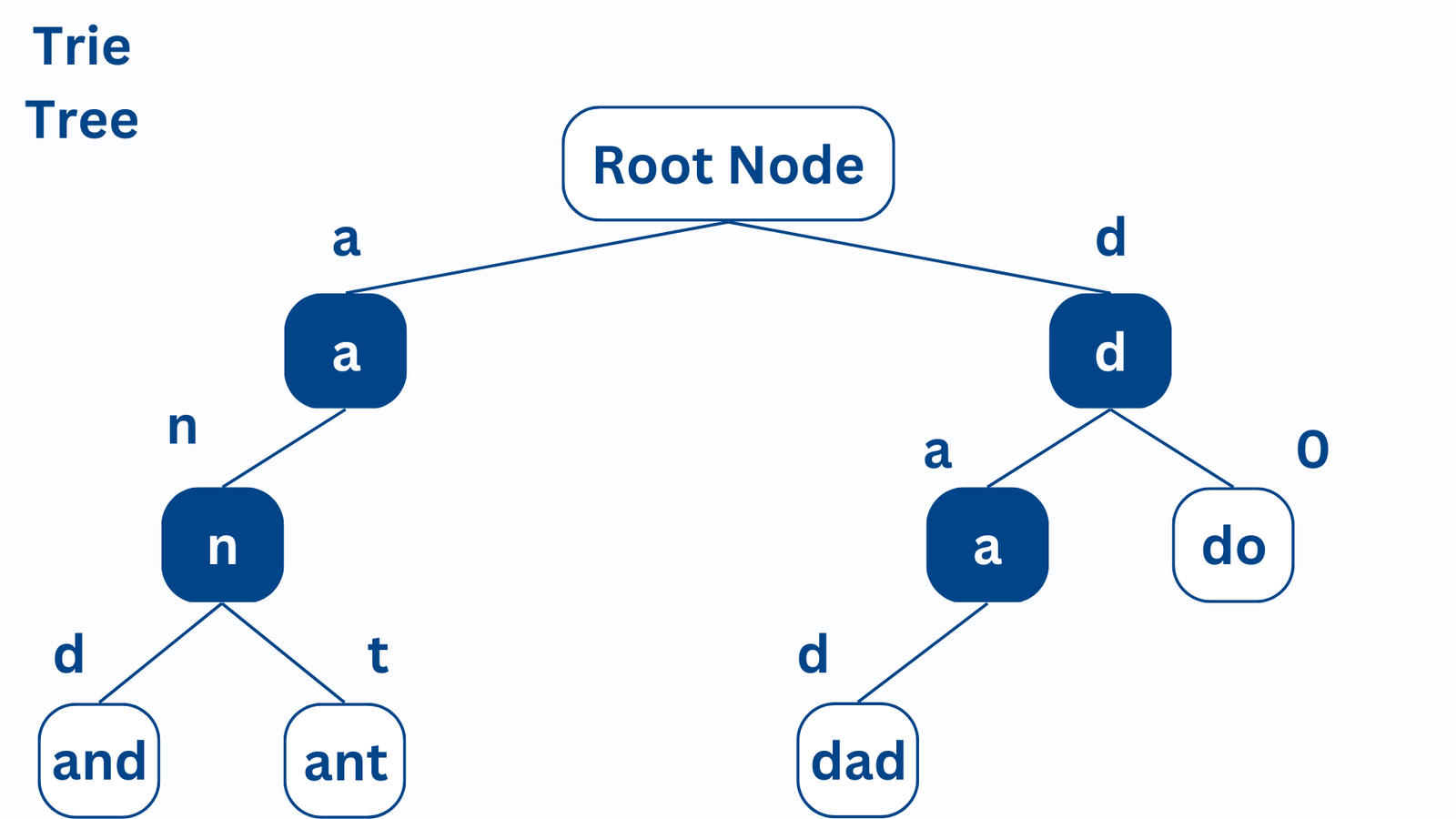
In a Trie tree, each node represents a single character of a string, and each edge represents a character link between the nodes. The root node represents an empty string, and the leaf nodes represent the end of a word.

Trie tree is an efficient data structure for searching for strings, as it allows for fast prefix matching. It also has a space-efficient structure, as it can store strings with similar prefixes in the same branch, reducing the overall space required to store the data.

How does a Trie Tree work?

A Trie tree consists of a root node and many child nodes. Each node represents a prefix of a word, and the edges between the nodes represent the characters of the words. A Trie tree allows us to search for a string by traversing down the tree, following the path of its characters.

Creating a Trie Tree

To create a Trie tree, we start with an empty root node. Then, for each string in the set, we insert the characters one by one by traversing down the tree, creating new nodes if necessary.

Searching in a Trie Tree

Searching in a Trie tree is done by traversing down the tree, following the path of the characters in the string we want to search. If we reach a node that represents the last character of the string, then the string exists in the Trie tree. Otherwise, the string does not exist.

Time Complexity of Trie Tree Operations

  • Insertion: O(n), where n is the length of the string
  • Search: O(n), where n is the length of the string
  • Deletion: O(n), where n is the length of the string

Advantages of Trie Tree

  • Efficient search for strings
  • Space-efficient for storing strings with similar prefixes
  • Easy to implement
  • Supports prefix matching

Implementation of Trie Tree

Trie tree can be implemented using an array or a linked list. Here, we will discuss the implementation using a linked list.

Trie Node

Each node in the Trie tree is represented by a struct that contains the following fields:

struct TrieNode {
    char val;
    bool isEndOfWord;
    struct TrieNode* children[ALPHABET_SIZE];
};

Here, val is the character that the node represents, isEndOfWord is a boolean flag that indicates whether the node represents the end of a word, and children is an array of pointers to its child nodes.

Insertion

To insert a string into the Trie tree, we start with the root node and traverse down the tree, creating new nodes if necessary. Once we reach the end of the string, we mark the last node as the end of a word.

void insert(struct TrieNode* root, char* key) {
    struct TrieNode* p = root;
    for(int i=0; i<strlen(key); i++) {
        int index = key[i] - 'a';
        if(!p->children[index]) {
            p->children[index] = getNode(key[i]);
        }
        p = p->children[index];
    }
    p->isEndOfWord = true;
}

Deletion

To delete a string from the Trie tree, we start with the root node and traverse down the tree, following the path of the characters in the string. Once we reach the end of the string, we mark the last node as not the end of a word. If the last node has no children, we delete it and continue deleting the parent nodes until we reach a node with children or a node that represents the end of another word.

bool delete(struct TrieNode* root, char* key) {
    if(!root || !key) {
        return false;
    }
    struct TrieNode* p = root;
    struct TrieNode* parent = NULL;
    for(int i=0; i<strlen(key); i++) {
        int index = key[i] - 'a';
        if(!p->children[index]) {
            return false;
        }
        parent = p;
        p = p->children[index];
    }
    if(!p->isEndOfWord) {
        return false;
    }
    p->isEndOfWord = false;
    if(isEmpty(p)) {
        deleteHelper(parent, p, key, 0);
    }
    return true;
}

Applications of Trie Tree

Trie tree has many applications, some of which are:

  • Autocomplete and spelling suggestions
  • IP routing and longest prefix matching
  • Text indexing and searching
  • Finding words in a dictionary
  • Compressing data
  • Implementing symbol tables

Conclusion

Trie tree is a powerful data structure that is widely used in computer science for storing and searching for strings efficiently. In this article, we have covered everything you need to know about Trie tree – from its definition to its implementation and uses. We hope that this article has helped you understand Trie tree better.

FAQs

  1. What is a Trie tree? A: Trie tree, also known as Prefix tree, is a tree-based data structure used to store and search for strings efficiently.
  2. What are the advantages of Trie tree? A: The advantages of Trie tree include efficient search for strings, space-efficiency for storing strings with similar prefixes, easy implementation, and support for prefix matching.
  3. How do you implement Trie tree? A: Trie tree can be implemented using an array or a linked list. The implementation using a linked list is discussed in detail in this article.
  4. What are the applications of Trie tree? A: The applications of Trie tree include autocomplete and spelling suggestions, IP routing and longest prefix matching, text indexing and searching, finding words in a dictionary, compressing data, and implementing symbol tables.
  5. Can Trie tree be used to search for substrings? A: Yes, Trie tree can be used to search for substrings by traversing down the tree and checking for the existence of the substring.
JOIN OUR NEWSLETTER
And get notified everytime we publish a new blog post.