1. Introduction

In computer science, data structures are an essential component of algorithms and software design. Data structures allow for efficient storage and retrieval of information, making them critical for modern computing. AVL trees are one such data structure that offers optimal performance for various applications.

2. What are AVL Trees?

Definition

An AVL tree is a self-balancing binary search tree, where the height of the left and right subtrees of any node differ by at most one. Additionally, each subtree of an AVL tree is itself an AVL tree.

AVL Tree Data Structure By Learn Loner

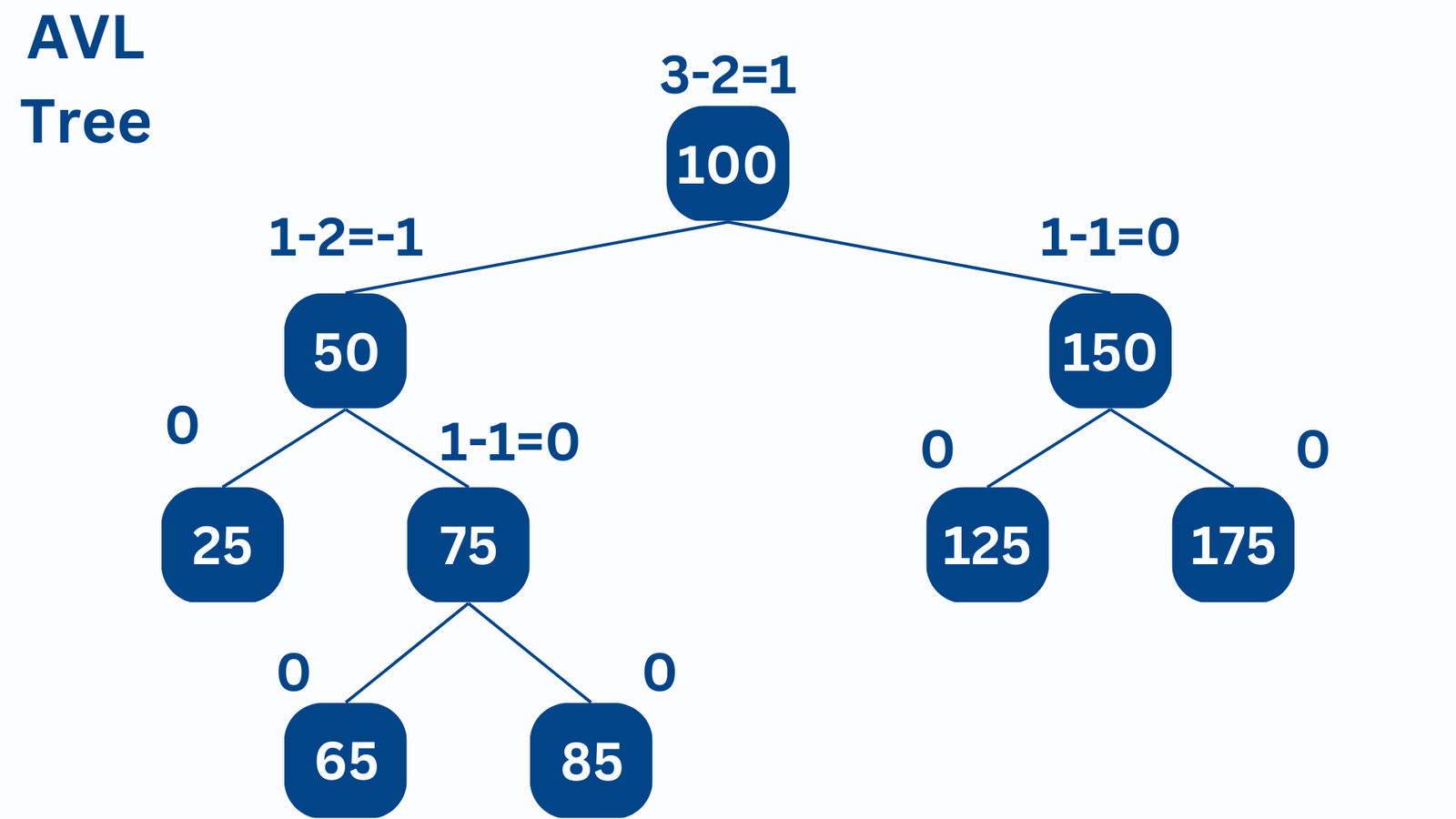
Properties

AVL trees have the following properties:

  • They are binary search trees, meaning that the left child of a node has a value less than or equal to the parent, and the right child has a value greater than or equal to the parent.
  • The height of an AVL tree is logarithmic, providing efficient searching, insertion, and deletion operations.
  • AVL trees are self-balancing, meaning that after any operation that modifies the tree, the height balance is maintained.

3. AVL Tree Operations

Insertion

To insert a new node into an AVL tree, we follow the same steps as a binary search tree. However, after the insertion, we must check the balance of the tree and rotate the tree if necessary to maintain the AVL balance property. There are four types of rotations for AVL trees, single left rotation, single right rotation, double left rotation, and double right rotation.

Deletion

To delete a node from an AVL tree, we first search for the node to remove. Then, we use the same steps as a binary search tree to delete the node. After deletion, we must check the balance of the tree and rotate it if necessary to maintain the AVL balance property.

Traversal

AVL trees support various traversal methods, including in-order, pre-order, and post-order traversals. In-order traversal of an AVL tree produces sorted output.

4. AVL Tree Applications

AVL trees have numerous applications, including:

Database indexing

AVL trees are commonly used in database indexing to speed up search queries by providing a fast access path to data.

Compiler design

AVL trees are used in compiler design to build and optimize syntax trees for efficient code generation.

Network routing

AVL trees are used in network routing algorithms to quickly find the shortest path between two nodes.

5. Advantages and Disadvantages of AVL Trees

Advantages

  • AVL trees provide efficient searching, insertion, and deletion operations.
  • AVL trees ensure that the height of the tree remains logarithmic, making them suitable for applications that require optimal performance.

Disadvantages

  • AVL trees require more rotations than other self-balancing trees, making them less efficient.
  • AVL trees are more complex to implement than other binary search trees.

AVL Tree

  • AVL trees are more balanced than red-black trees, meaning that they require fewer rotations to maintain the balance property.
  • AVL trees are better suited for applications that require frequent search operations.
  • AVL trees have a more rigid balance requirement than red-black trees, meaning that they may be less flexible in certain situations.

Red-Black Tree

  • Red-black trees require fewer rotations than AVL trees to maintain balance, making them more efficient in some situations.
  • Red-black trees are better suited for applications that require more frequent insertions and deletions.
  • Red-black trees are more flexible than AVL trees, meaning that they can be more easily adapted to certain situations.

Ultimately, the choice between AVL trees and red-black trees will depend on the specific application and the performance requirements.

7. Conclusion

AVL trees are a powerful data structure that provide efficient searching, insertion, and deletion operations. They are commonly used in applications such as database indexing, compiler design, and network routing. By maintaining a logarithmic height and self-balancing, AVL trees offer optimal performance for a wide range of applications.

8. FAQs

  1. What is the advantage of using an AVL tree over a regular binary search tree?
    • AVL trees ensure that the height of the tree remains logarithmic, providing efficient searching, insertion, and deletion operations.
  2. How are AVL trees balanced?
    • AVL trees are self-balancing, meaning that after any operation that modifies the tree, the height balance is maintained.
  3. What are some applications of AVL trees?
    • AVL trees are commonly used in database indexing, compiler design, and network routing.
  4. How do AVL trees compare to red-black trees?
    • AVL trees are more balanced than red-black trees, while red-black trees require fewer rotations than AVL trees to maintain balance.
  5. Which is better, AVL trees or red-black trees?
    • The choice between AVL trees and red-black trees will depend on the specific application and the performance requirements.
JOIN OUR NEWSLETTER
And get notified everytime we publish a new blog post.